The vector 2-norm

The length of a vector is most commonly measured by the “square root of the sum of the squares of the elements”. It is also known as the Euclidean norm.

$$
\begin{align}
\mathbf{x} =
\begin{bmatrix}
x_1 \\
x_2 \\
… \\
x_n
\end{bmatrix}
\Rightarrow
||\mathbf{x}||_2 = \sqrt{x_1^2 + x_2^2 + \dots x_n^2}
\end{align}
$$

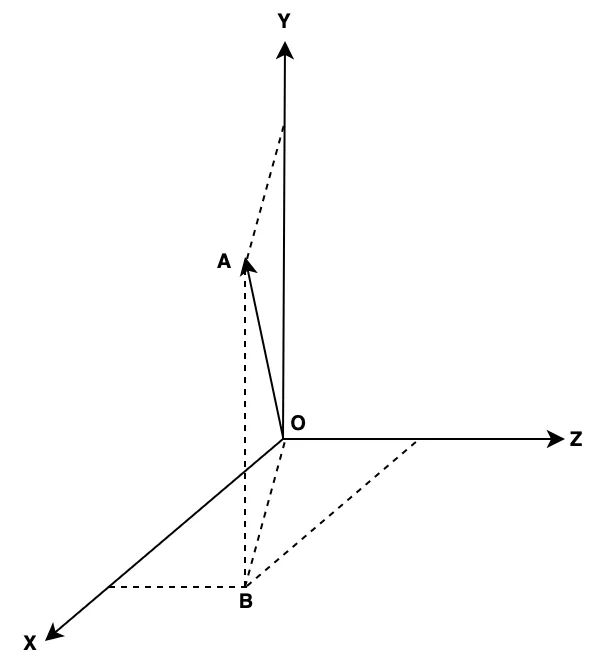
Let’s try to see a specific example. Given a vector & show it on the coordinate system (x, y, z)

$$
\begin{align}
\mathbf{x} =
\begin{bmatrix}
5 \\
8 \\
3
\end{bmatrix}
\end{align}
$$

We can see that A point describes the coordinate of \(\mathbf{x}\) vector. Using Pythagorean theorem, we can calculate the length of this vector

$$
\begin{align}
OB^2 &= 3^2 + 5^2 \\
\Rightarrow OA^2 &= OB^2 + AB^2 = 3^2 + 5^2 + 8^2 \\
\Rightarrow OA &= \sqrt{3^2 + 5^2 + 8^2}
\end{align}
$$

Based on this, with \(p >= 1\) the formula to get norm \(p\) is

$$
||\mathbf{x}||_p = (|x_1|^p + |x_2|^p + \dots |x_n|^p)^{\frac{1}{p}}
$$