What is Gradient Descent? You can read more this post.
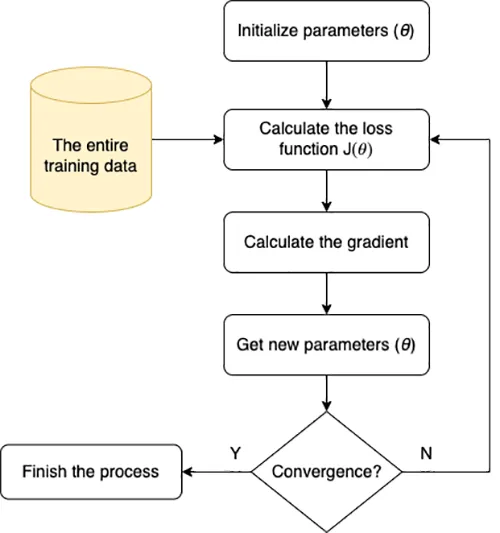
1. Batch Gradient Descent (BGD)
Basically, Gradient Descent is an algorithm to look for the global minimum of a loss function. The formula of loss function:
$$
\begin{align}
\mathcal{L}(\mathbf{w}) = \frac{1}{2N}\sum_{i=1}^N (y_i – \mathbf{x}_i^T\mathbf{w}_i)^2
\end{align}
$$
In order to build the loss function, we will use the whole training data (from 1 to N). When we already have the loss function, we use the gradient descent to find the minimum of loss function by using:
$$
\begin{align}
\theta = \theta – \eta \nabla_{\theta}J(\theta)
\end{align}
$$
\(\nabla_{\theta}J(\theta)\) is the derivative of loss function at \(\theta\). It means that each update will recompute the gradient based on all training data. It’s not appropriate when we want to update online with the large training data.
But the simplicity of BGD makes it a good choice for training on datasets that are not too large, allowing for precise computation of the gradient of the loss function across the whole dataset.
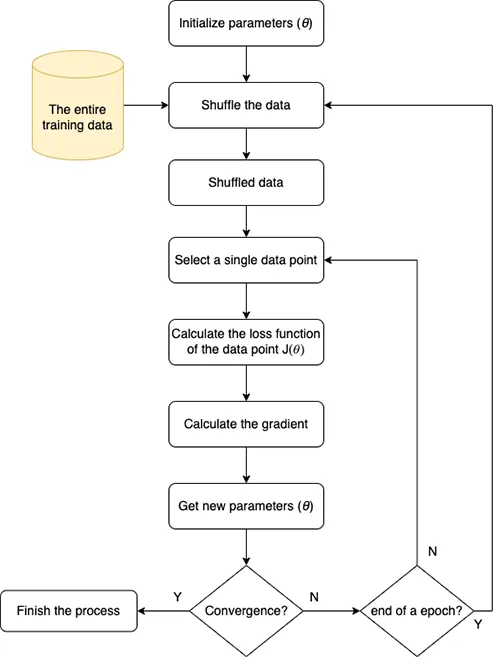
2. Stochastic Gradient Descent (SGD)
SGD is useful for training on the large datasets & you want to have an “online” training model. The main difference between SGD & BGD is that SGD only uses a single data point instead of the entire training data on each update.
Because we only select a single data point so we need to “shuffle” the training data at the beginning of each “epoch” that makes sure the order of the data does not affect the optimization process.
The loss function of a single data point:
$$
\begin{align}
\mathcal{L}(\mathbf{w};x_i;y_i) = \frac{1}{2} (y_i – \mathbf{x}_i\mathbf{w})^2
\end{align}
$$
The update formula is:
$$
\begin{align}
\theta = \theta – \eta \nabla_{\theta}J(\theta;x_i;y_i)
\end{align}
$$
\(\nabla_{\theta}J(\theta;x_i;y_i)\) is the derivative of loss function at a single data point \((x_i;y_i)\)
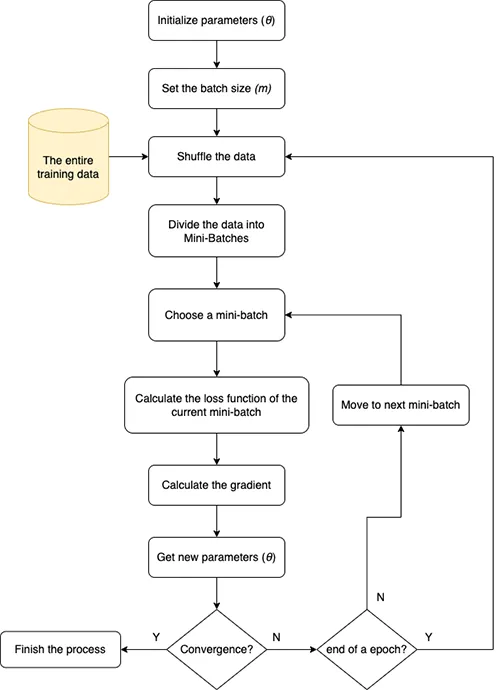
3. Mini-batch Gradient Descent
Mini-batch gradient descent is a balance solution between BGD & SGD. It’s similar to SGD but instead of using 1 single data point, we will use “n” data points. n > 1 but it’s much smaller than N (total training data points).
With m is mini-batch of size. The mini-batch loss function formula:
\[ \mathcal{L}_{\text{mini-batch}}(\theta) = \frac{1}{m} \sum_{i=1}^{m} L(y_i, \hat{y}_i) \]
The gradient descent update rule for mini-batch:
\[ \theta = \theta – \alpha \frac{1}{m} \sum_{i=1}^{m} \nabla_\theta L(\theta; x_i, y_i) \]