Cross-entropy is a commonly used loss function in machine learning, particularly in classification tasks, to measure the difference between two probability distributions. It is used to quantify the error between the actual distribution of the labels and the predicted distribution by a model.
\[ H(p, q) = – \sum_{i=1}^{n} p(x_i) \log(q(x_i)) \]
- \(p(x_i)\): the true probability of class \(i\) (usually 0 or 1 in classification tasks)
- \(q(x_i)\): the predicted probability for class \(i\)
- \(n\): the number of classes
1. Basic sample
Suppose you’re predicting the outcome of a football match, and there are three possible outcomes:
- Team A wins
- Team B wins
- Draw
Let’s assume the true result is that Team A wins:
- Team A wins: 1
- Team B wins: 0
- Draw: 0
Now, suppose your model predicts the following probabilities for the outcomes:
- Team A wins: 0.6
- Team B wins: 0.3
- Draw: 0.1
The cross-entropy would be calculated as follows:
\[ H(p, q) = -(1 \cdot \log(0.6) + 0 \cdot \log(0.3) + 0 \cdot \log(0.1)) \]
\[ \Rightarrow H(p, q) = -\log(0.6) \]
\[ \Rightarrow H(p, q) \approx -(-0.2218) = 0.2218 \]
So the cross-entropy loss for this prediction would be approximately 0.2218
2. Logarithm Function
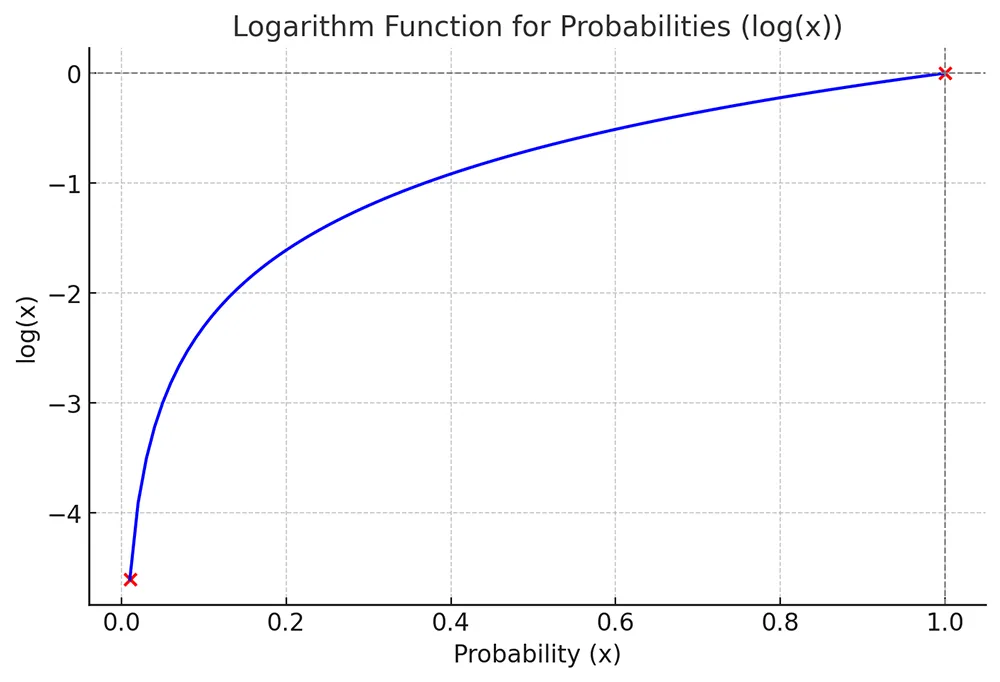
- At \(x = 1\) => \(\log(1) = 0\)
- As \(x\) decreases (closer to 0) => \(\log(x)\) becomes more negative
Based on the above properties, we use the logarithm in the cross-entropy formula is to penalize incorrect predictions more strongly.
- Logarithms turn small probabilities into large negative values, heavily penalizing wrong predictions.
- If the predicted probability of the true class is high (close to 1), the logarithm yields a value close to 0, meaning low loss and rewarding accurate predictions.
- The logarithmic function provides smooth, differentiable output, which helps optimization algorithms (like gradient descent) efficiently update model weights during training.
