Backpropagation is a fundamental algorithm used in training artificial neural networks in machine learning. It works by minimizing the error (or loss) between the predicted output of the network and the actual desired output through a process called gradient descent.
1. The steps
1.1. Forward Pass
Input data is fed into the network, where it passes through multiple layers of neurons, each applying a mathematical transformation. The output is compared to the actual target value to compute the error (using a loss function).
1.2. Error Calculation
The error between the predicted output and the actual value is calculated.
1.3. Backward Pass
The error is propagated back through the network, layer by layer, in the reverse direction (from output to input). During this process, partial derivatives of the error with respect to each weight and bias are computed using the chain rule of calculus. These derivatives show how the weights contributed to the error.
1.4. Gradient Descent
The gradients are used to adjust the weights and biases in the network. The goal is to reduce the error by updating the weights in the direction that minimizes the loss. This adjustment is done using a learning rate, which controls how much to change the weights at each step.
1.5. Repeat the Process
The forward and backward passes are repeated for many iterations (epochs) until the network’s weights are optimized, minimizing the error as much as possible.
2. Basic example
2.1. Network Structure
- 1 input layer (2 neurons)
- 1 hidden layer (2 neurons)
- 1 output layer (1 neuron)
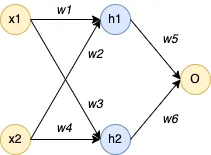
2.2. Problem
- Input: \( [x_1, x_2] = [0.05, 0.10] \)
- Output: 0.01
- Learning Rate: 0.5
2.3. Random Initial Weights
- Weights between input and hidden layer: \( w_1 = 0.15, w_2 = 0.20, w_3 = 0.25, w_4 = 0.30 \)
- Weights between hidden and output layer: \( w_5 = 0.40, w_6 = 0.45 \)
2.4. Activation Function
- Sigmoid function: \( \sigma(x) = \frac{1}{1 + e^{-x}} \)
2.5. Forward Pass
2.5.1. Input to Hidden Layer
- Hidden Neuron 1:
\[ h_1 = \sigma(x_1 \cdot w_1 + x_2 \cdot w_2) = \sigma(0.05 \cdot 0.15 + 0.10 \cdot 0.20) = \sigma(0.0075 + 0.02) = \sigma(0.0275) = 0.5069 \]
- Hidden Neuron 2:
\[ h_2 = \sigma(x_1 \cdot w_3 + x_2 \cdot w_4) = \sigma(0.05 \cdot 0.25 + 0.10 \cdot 0.30) = \sigma(0.0125 + 0.03) = \sigma(0.0425) = 0.5106 \]
2.5.2. Hidden to Output Layer
\[ Output = \sigma(h_1 \cdot w_5 + h_2 \cdot w_6) = \sigma(0.5069 \cdot 0.40 + 0.5106 \cdot 0.45) = \sigma(0.2028 + 0.2298) = \sigma(0.4326) = 0.6069 \]
2.6. Error Calculation (Loss)
Use Mean Squared Error (MSE)
\[ E = \frac{1}{2} (t – o)^2 \]
- is the actual value.
- \(o\) is the output (predicted) value.
\[ E = \frac{1}{2}(t – o)^2 = \frac{1}{2}(0.01 – 0.6069)^2 = \frac{1}{2}(-0.5969)^2 = 0.178 \]
2.7. Backpropagation
2.7.1. Output to Hidden Layer
- Calculate gradient of the error with respect to the output:
\[ \frac{\partial E}{\partial o} = \frac{\partial}{\partial o} \left( \frac{1}{2} (t – o)^2 \right) \]
\[ \Rightarrow \frac{\partial E}{\partial o} = \frac{1}{2} \cdot \frac{\partial}{\partial o} \left( (t – o)^2 \right) \]
Apply the chain rule, we have
\[ \frac{\partial}{\partial o} \left( (t – o)^2 \right) = 2(t – o) \cdot \frac{\partial}{\partial o}(t – o) \]
Since \(t\) is a constant and does not depend on \(o\)
\[ \Rightarrow \frac{\partial E}{\partial o} = \frac{1}{2} \cdot 2(t – o) \cdot (-1) \]
\[ \Rightarrow \frac{\partial E}{\partial o} = o – t \]
\[ \Rightarrow \frac{\partial E}{\partial o} = o – t = 0.6069 – 0.01 = 0.5969 \]
- Calculate gradient of the output with respect to the net input (the derivative of Sigmoid function):
\[ \frac{\partial o}{\partial net_o} = o(1 – o) = 0.6069(1 – 0.6069) = 0.2384 \]
- Calculate total gradient for the output neuron:
\[ \delta_o = \frac{\partial E}{\partial net_o} = \frac{\partial E}{\partial o} \cdot \frac{\partial o}{\partial net_o} = 0.5969 \cdot 0.2384 = 0.1423 \]
- Adjust weights between hidden and output neurons (weights in neural network):
\[ \Delta w_5 = -\eta \cdot \delta_o \cdot h_1 = -0.5 \cdot 0.1423 \cdot 0.5069 = -0.036 \]
\[ \Delta w_6 = -\eta \cdot \delta_o \cdot h_2 = -0.5 \cdot 0.1423 \cdot 0.5106 = -0.0363 \]
- Update weights:
\[ w_5 = 0.40 – 0.036 = 0.364 \]
\[ w_6 = 0.45 – 0.0363 = 0.4137 \]
2.7.2. Hidden Layer to Input Layer
- Calculate the gradient for the hidden neurons:
\[ \frac{\partial E}{\partial net_{h1}} = \frac{\partial E}{\partial h1} \cdot \frac{\partial h1}{\partial net_{h1}} \]
\[ \Rightarrow \frac{\partial E}{\partial net_{h1}} = \frac{\partial E}{\partial net_o} \cdot \frac{\partial net_o}{\partial h1} \cdot \frac{\partial h1}{\partial net_{h1}} \]
\[ \Rightarrow \frac{\partial E}{\partial net_{h1}} = \delta_o \cdot \frac{\partial net_o}{\partial h1} \cdot h1(1-h1) \]
We have \(net_o = h_1w_5 + h_2w_6 \) so \( \frac{\partial net_o}{\partial h1} = w_5 \)
\[ \Rightarrow \delta_{h1} = \frac{\partial E}{\partial net_{h1}} = \delta_o \cdot w_5 \cdot h1(1-h1) \]
\[ \Rightarrow \delta_{h1} = 0.1423 \cdot 0.40 \cdot 0.5069(1 – 0.5069) = 0.0147 \]
Similarly we can calculate
\[ \delta_{h2} = \frac{\partial E}{\partial net_{h2}} = \delta_o \cdot w_6 \cdot h2(1-h2) \]
\[ \Rightarrow \delta_{h2} = 0.1423 \cdot 0.45 \cdot 0.5106(1 – 0.5106) = 0.0158 \]
- Adjust weights between input and hidden neurons:
\[ \Delta w_1 = -\eta \cdot \delta_{h1} \cdot x_1 = -0.5 \cdot 0.0147 \cdot 0.05 = -0.0004 \]
\[ \Delta w_2 = -\eta \cdot \delta_{h1} \cdot x_2 = -0.5 \cdot 0.0147 \cdot 0.10 = -0.0007 \]
\[ \Delta w_3 = -\eta \cdot \delta_{h2} \cdot x_1 = -0.5 \cdot 0.0158 \cdot 0.05 = -0.0004 \]
\[ \Delta w_4 = -\eta \cdot \delta_{h2} \cdot x_2 = -0.5 \cdot 0.0158 \cdot 0.10 = -0.0008 \]
- Update weights:
\[ w_1 = 0.15 – 0.0004 = 0.1496 \]
\[ w_2 = 0.20 – 0.0007 = 0.1993 \]
\[ w_3 = 0.25 – 0.0004 = 0.2496 \]
\[ w_4 = 0.30 – 0.0008 = 0.2992 \]
2.7.3. Repeat
This process is repeated for many iterations until the error becomes small enough, meaning the network has learned the relationship between inputs and outputs.
3. Pytorch Code
import torch
import torch.nn as nn
import torch.optim as optim
# Set the manual seed for reproducibility
torch.manual_seed(42)
# Define the network structure
class SimpleNeuralNetwork(nn.Module):
def __init__(self):
super(SimpleNeuralNetwork, self).__init__()
# Input to Hidden layer (2 neurons in hidden layer)
self.hidden = nn.Linear(2, 2)
# Hidden to Output layer (1 neuron in output layer)
self.output = nn.Linear(2, 1)
# Sigmoid activation function
self.sigmoid = nn.Sigmoid()
def forward(self, x):
h = self.sigmoid(self.hidden(x)) # Hidden layer with sigmoid activation
o = self.sigmoid(self.output(h)) # Output layer with sigmoid activation
return o
# Example problem parameters
x1, x2 = 0.05, 0.10
target = torch.tensor([0.01], dtype=torch.float32) # Target output reshaped to match output size
# Input data
inputs = torch.tensor([x1, x2], dtype=torch.float32).unsqueeze(0) # Adding batch dimension
# Create the network instance
network = SimpleNeuralNetwork()
# Initialize the weights manually (as provided in the problem)
with torch.no_grad():
network.hidden.weight = torch.nn.Parameter(torch.tensor([[0.15, 0.20], [0.25, 0.30]], dtype=torch.float32))
network.hidden.bias = torch.nn.Parameter(torch.zeros(2)) # No biases provided, so initialize to 0
network.output.weight = torch.nn.Parameter(torch.tensor([[0.40, 0.45]], dtype=torch.float32))
network.output.bias = torch.nn.Parameter(torch.zeros(1)) # No bias provided, so initialize to 0
# Define the loss function (Mean Squared Error)
criterion = nn.MSELoss()
# Define the optimizer (using SGD with the provided learning rate)
optimizer = optim.SGD(network.parameters(), lr=0.5)
# Perform one forward pass
output = network(inputs).squeeze() # Remove extra dimensions if necessary
# Calculate the loss
loss = criterion(output, target)
# Print the forward pass output and loss
print("Output:", output.item())
print("Loss:", loss.item())
# Perform one backward pass (backpropagation)
optimizer.zero_grad() # Clear previous gradients
loss.backward() # Compute gradients
optimizer.step() # Update weights
# Print updated weights after backpropagation
print("Hidden layer weights:", network.hidden.weight)
print("Output layer weights:", network.output.weight)
# Perform another forward pass to see updated output
updated_output = network(inputs).squeeze() # Ensure the output shape matches the target
updated_loss = criterion(updated_output, target)
# Print the updated output and loss after backpropagation
print("Updated output:", updated_output.item())
print("Updated loss:", updated_loss.item())
# The result
Output: 0.606477677822113
Loss: 0.35578563809394836
Hidden layer weights: Parameter containing:
tensor([[0.1493, 0.1986],
[0.2492, 0.2984]], requires_grad=True)
Output layer weights: Parameter containing:
tensor([[0.3278, 0.3773]], requires_grad=True)
Updated output: 0.5532403588294983
Updated loss: 0.2951101064682007
