Activation Functions

Activation Functions are mathematical functions used in artificial neural networks (ANNs) to determine whether a neuron should be activated or not. They allow the neural network to capture more complex relationships between inputs and outputs, which wouldn’t be possible with linear transformations alone.

1. Linear

The Linear Activation Function is the simplest type of activation function used in neural networks. It produces an output that is directly proportional to the input, without introducing any non-linearity into the model.

\[ f(x) = x \]

• $\backslash (f(x)\backslash )$ is the output of the linear function.
• \(x\) is the input to the function.

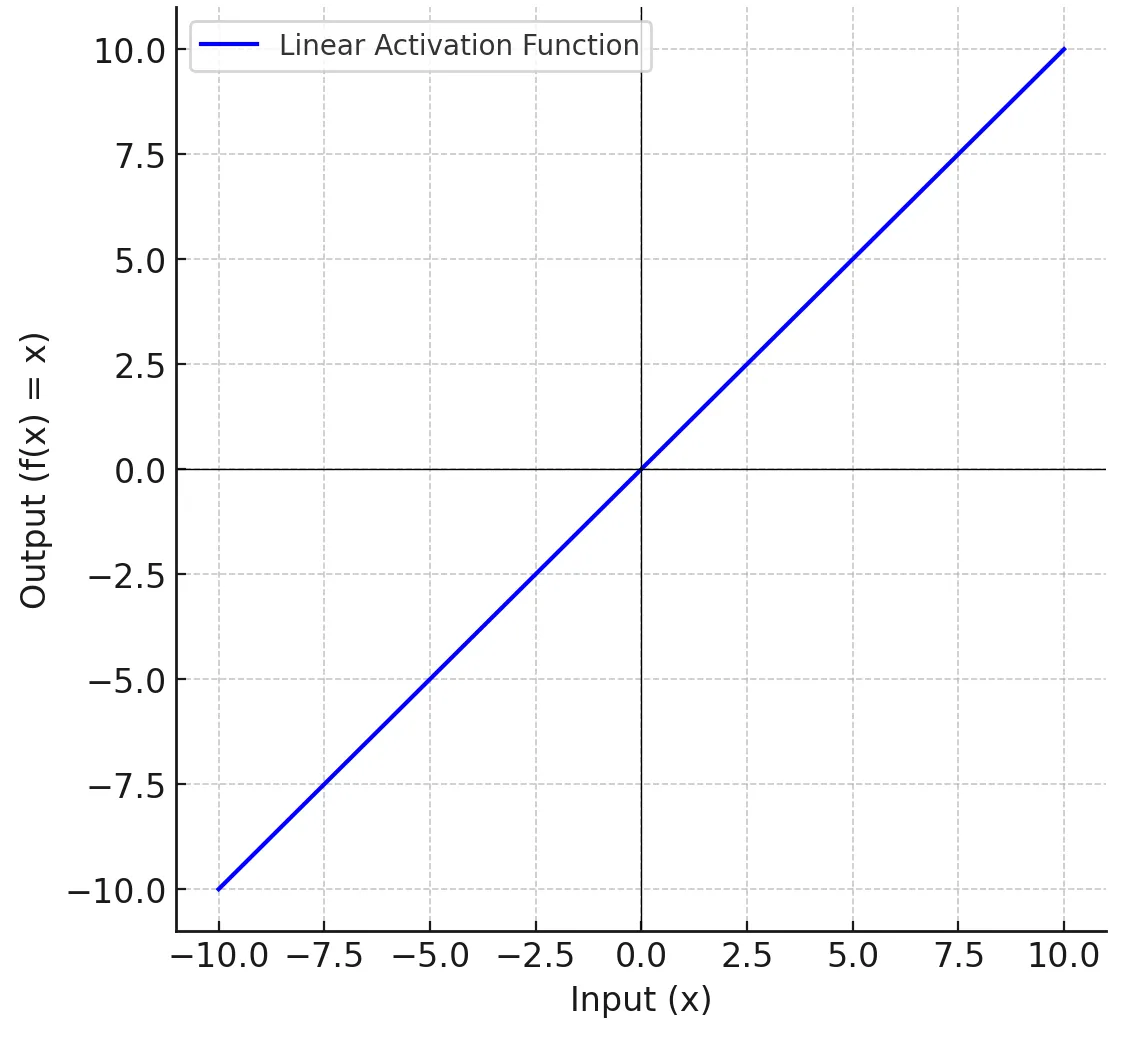
The Linear Activation Function is typically used in the following scenarios:

1.1. Regression Problems

Linear activation functions are often used in the output layer of a neural network for regression tasks, where the goal is to predict a continuous value (e.g. predicting house prices, stock prices, or other real-valued quantities).

In regression, the network needs to output a continuous number, and using a linear function allows the model to produce any real value, which suits the nature of regression problems.

1.2. Simple Linear Models

If the data or task at hand can be modeled by a simple linear function, using a linear activation function across the entire network may be appropriate.

In cases where the relationship between input and output is strictly linear, no non-linearity is required, so a linear activation function suffices.

1.3. Output Layer in Some Networks

Even in deep networks, a linear activation may be used in the output layer when a real, unbounded number is required as the final output.

Non-linear activation functions (like ReLU or Sigmoid) are useful in hidden layers to introduce complexity, but if the task requires a real-valued output, linear activation is needed at the end.

2. Sigmoid

The Sigmoid Activation Function is a commonly used activation function in neural networks. It maps input values to an output range between 0 and 1, making it useful for tasks where the output is a probability or a binary classification.

\[ f(x) = \frac{1}{1 + e^{-x}} \]

• $\backslash (f(x)\backslash )$ is the output of the sigmoid function.
• \(x\) is the input to the function.
• \(e\) is Euler’s number.

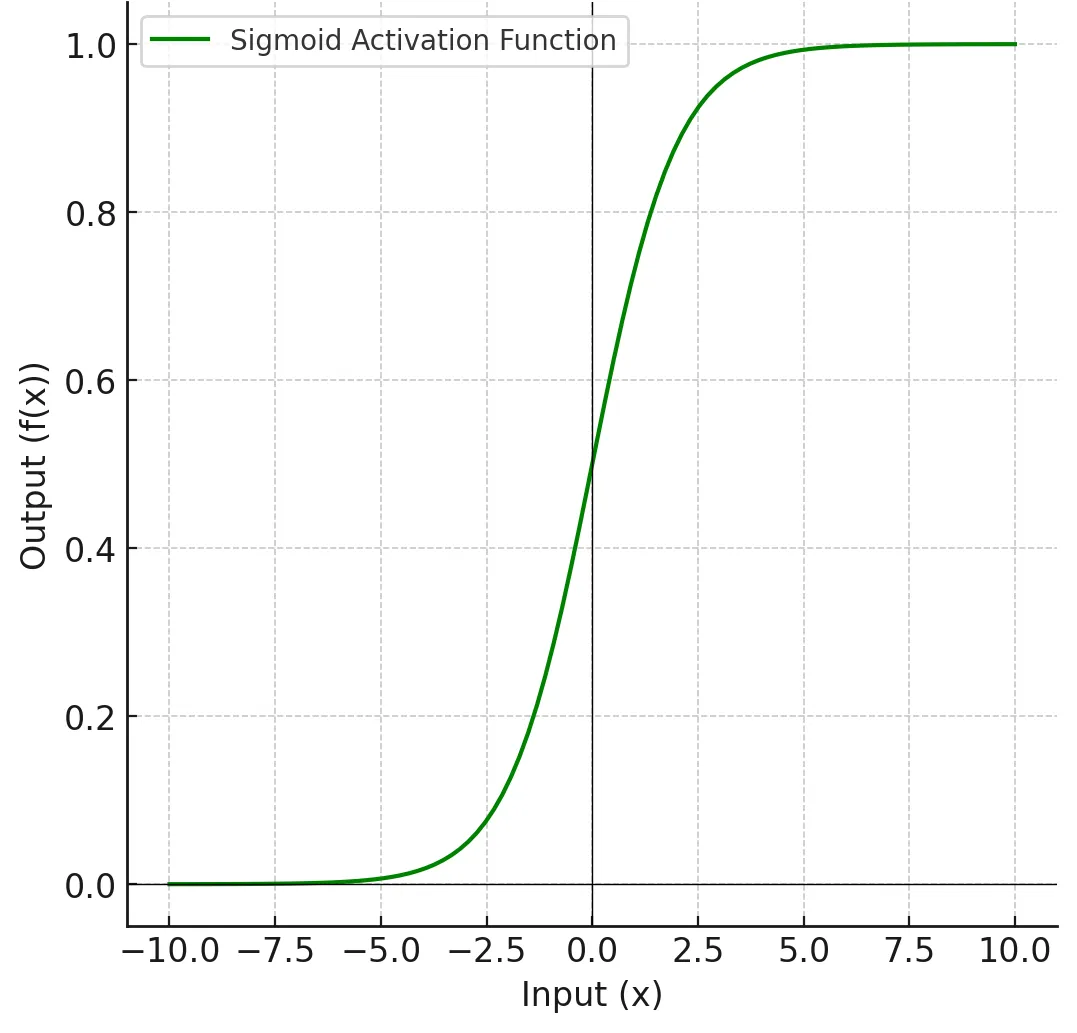
The Sigmoid Activation Function is used in several specific scenarios, primarily due to its ability to map input values to a range between 0 and 1

2.1. Binary Classification Problems

The sigmoid function is often used in the output layer of a neural network for binary classification tasks, where the goal is to predict one of two possible outcomes (e.g., yes/no, true/false). Because the sigmoid function outputs values between 0 and 1, it can be interpreted as a probability.

2.2. Logistic Regression

Logistic regression, which is a binary classification algorithm, typically uses the sigmoid function in its core to map predictions to probabilities. The sigmoid function transforms the raw output (logits) into a probability, which can be thresholded to decide the predicted class (e.g., values above 0.5 might be classified as 1, and below as 0).

2.3. Output Layer of Neural Networks

In neural networks, the sigmoid activation function is frequently used in the output layer when the model needs to produce a probability-like output. It squashes the output to a range between 0 and 1, making it ideal for problems where each output neuron represents a separate binary outcome (multi-label classification).

2.4. Simpler Networks

Sigmoid functions can be used in shallow networks or small models where the vanishing gradient problem is not a major concern. In smaller models, the gradient-related issues of the sigmoid function are less pronounced, and it provides smooth and interpretable outputs.

3. Tanh

Tanh Activation Function is a popular activation function used in neural networks, especially for hidden layers. It is similar to the sigmoid function but differs in that it maps input values to an output range between -1 and 1, instead of 0 and 1.

\[ f(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}} \]

• \(f(x)\) is the tanh function output.
• \(x\) is the input to the neuron.
• \(e\) is Euler’s number.

The derivative of the tanh function is important for backpropagation in neural networks:

\[ f'(x) = 1 – \tanh^2(x) \]

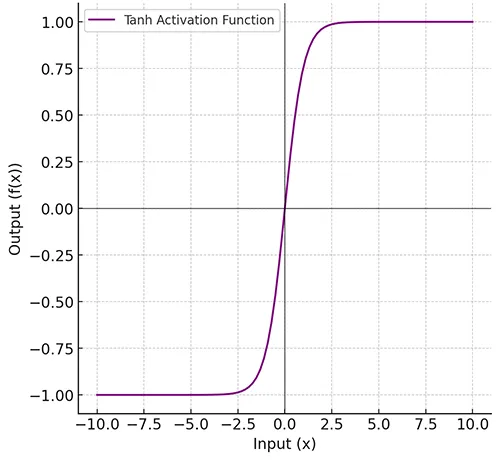
The Tanh Activation Function is used in specific scenarios due to its properties of mapping input values to the range of -1 to 1, which can be beneficial in various neural network architectures.

3.1. Hidden Layers of Neural Networks

Tanh is often used in the hidden layers of neural networks because it is zero-centered, meaning its output is balanced between negative and positive values. This can lead to faster learning compared to functions like Sigmoid, which outputs only positive values.

The zero-centered nature of Tanh allows the gradients to flow more effectively, which can help the network converge faster during training.

3.2. Binary Classification Tasks

Similar to the Sigmoid function, Tanh can be used in binary classification tasks, especially when the output layer is designed to predict two classes.

Tanh’s output range of -1 to 1 makes it easier to interpret strong negative and strong positive relationships between inputs and outputs, making it useful for tasks where a classification boundary is needed between two categories.

3.3. Recurrent Neural Networks (RNNs)

Tanh is commonly used in Recurrent Neural Networks (RNNs), especially in architectures like LSTMs (Long Short-Term Memory networks).

RNNs benefit from the smooth, non-linear mapping of the Tanh function. Since the function can output negative and positive values, it allows better control over the internal cell states in memory-based models, providing improved performance in handling sequential data like time series and natural language processing.

4. ReLU (Rectified Linear Unit)

The ReLU Activation Function is one of the most popular activation functions used in neural networks, especially for deep learning. It has become the default choice for most neural networks due to its simplicity and effectiveness in solving the vanishing gradient problem.

\[ f(x) = \max(0, x) \]

• $\backslash (f(x)\backslash )$ is the output of the ReLU function.
• \(x\) is the input to the neuron.

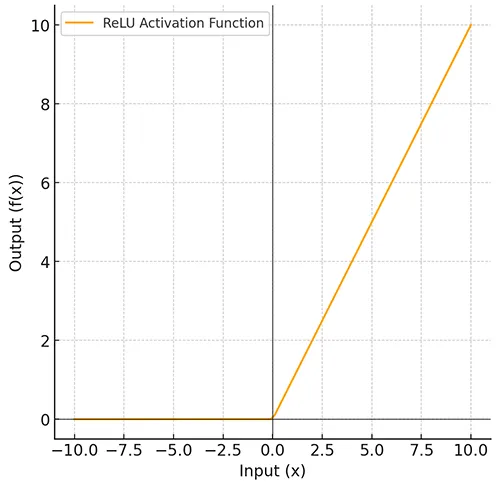
The ReLU Activation Function is widely used in deep learning, especially for training large and complex neural networks.

4.1. Hidden Layers in Deep Neural Networks

ReLU is most commonly used in the hidden layers of neural networks, particularly in deep learning architectures such as Convolutional Neural Networks (CNNs) and Fully Connected Networks.

ReLU introduces non-linearity while being computationally efficient, and it allows networks to train faster by avoiding issues like the vanishing gradient problem, which occurs with other functions like Sigmoid or Tanh.

4.2. Deep Convolutional Neural Networks (CNNs)

ReLU is the go-to activation function in the hidden layers of CNNs, used for tasks such as image recognition, object detection, and image segmentation.

The simplicity and efficiency of ReLU allow CNNs to extract complex features from image data quickly and effectively, without suffering from the gradient issues that hindered earlier activation functions.

4.3. Avoiding the Vanishing Gradient Problem

In deep networks, the vanishing gradient problem can slow down or even halt learning, particularly when using activation functions like Sigmoid or Tanh.

ReLU helps prevent this by providing a constant gradient for positive inputs. Since the gradient of ReLU is 1 for x > 0, it allows gradients to flow more effectively during backpropagation, enabling faster learning in deep networks.

4.4. When Negative Inputs Are Not Important

ReLU is suitable for tasks where negative input values to neurons are not significant or not expected to carry much information.

ReLU effectively “ignores” negative inputs by outputting zero for all negative values, making it efficient in focusing on positive signal propagation.

5. Leaky ReLU

The Leaky ReLU activation function is a variation of the standard ReLU function. While ReLU sets all negative values to zero, Leaky ReLU allows a small, non-zero gradient for negative inputs.

\[ f(x) = \begin{cases} x, & \text{if } x > 0 \\ \alpha x, & \text{if } x \leq 0 \end{cases} \]

• \(x\) is the input to the neuron.
• \(\alpha\) is a small constant (typically \(\alpha = 0.01\)), which controls the slope for negative input values.

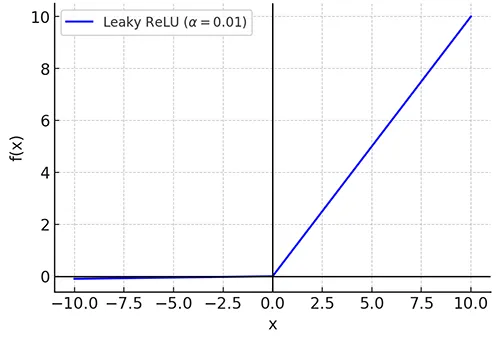
Leaky ReLU is used in neural networks to address some of the limitations of the standard ReLU activation function.

5.1. Avoiding Dying Neurons

Leaky ReLU ensures that neurons still receive some gradient even when the input is negative, preventing them from becoming completely inactive, unlike standard ReLU, which outputs zero for negative inputs.

5.2. Deep Neural Networks

In very deep networks, where the vanishing gradient problem is a concern, Leaky ReLU helps by maintaining a small gradient for negative values. This allows neurons to continue learning, even in deeper layers.

5.3. Unstable or Unreliable Gradients

If you observe that certain neurons are getting stuck or dying in training (particularly in networks with ReLU), switching to Leaky ReLU can help maintain smoother gradient flow, improving the training process.

5.4. When Negative Inputs Have Meaning

In cases where negative input values carry useful information for the network, Leaky ReLU allows these values to contribute to learning, unlike ReLU, which would discard them.

6. Softmax

The Softmax function is an activation function commonly used in neural networks, especially in the final layer of classification models for multi-class problems. It transforms raw output scores (logits) into probabilities, ensuring that they sum up to 1, making it suitable for tasks like multi-class classification.

The Softmax function for an input vector \(z\) with components \(z_1,z_2,\dots,z_n\) is given by:

\[ \sigma(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}} \]

• $\backslash (z\_i\backslash )$ is the i-th element of the input vector \(z\).
• \(e\) is the base of the natural logarithm.
• \(\sum_{j=1}^{n} e^{z_j}\)​ is the sum of exponentials of all input elements.

The Softmax activation function is typically used in neural networks when the task involves multi-class classification, where the goal is to assign an input to one of several categories. It is used in the output layer of the neural network to convert raw output values (logits) into a probability distribution over the possible classes.

6.1. Multi-Class Classification Problems

Softmax is primarily used when there are more than two classes to predict. For example, if you’re classifying images into 10 categories (e.g., digits 0–9), Softmax will output a probability distribution across all 10 categories.

It assigns probabilities to each class such that the sum of all probabilities equals 1, making it easier to interpret the model’s output as class probabilities.

6.2. Final Layer of the Neural Network

Softmax is generally applied in the final layer of the network. This allows the model to output probabilities that sum to 1, where the class with the highest probability is selected as the predicted class.

6.3. Multi-Class Logistic Regression

Softmax is often used in multi-class logistic regression models. The network learns a linear relationship for each class and applies Softmax to convert raw scores into probabilities.

6.4. Output Layer with Multiple Classes

If the network architecture includes an output layer where each neuron represents a distinct class, Softmax ensures that the output of each neuron is a probability associated with that class.