1. What is Cosine Similarity?
Cosine similarity is a mathematical measure that calculates the similarity between two non-zero vectors in an inner product space. It is commonly used in text analysis, recommendation systems, and machine learning to measure how similar two documents, feature vectors, or data points are.
\[ \text{cosine similarity} = \cos(\theta) = \frac{A \cdot B}{\|A\| \cdot \|B\|} \]
- \(A \cdot B\): Dot product of vectors A and B
- \(\|A\|\): Euclidean norm of vector A
- \(\|B\|\): Euclidean norm of vector B
Read more about Euclidean norm.
Cosine similarity measures the cosine of the angle between two vectors, ranging from -1 to 1. It tells us how similar two vectors are in terms of direction.
- 1: Perfect similarity
- 0: No similarity
- -1: Completely opposite
2. Prove Cosine Similarity
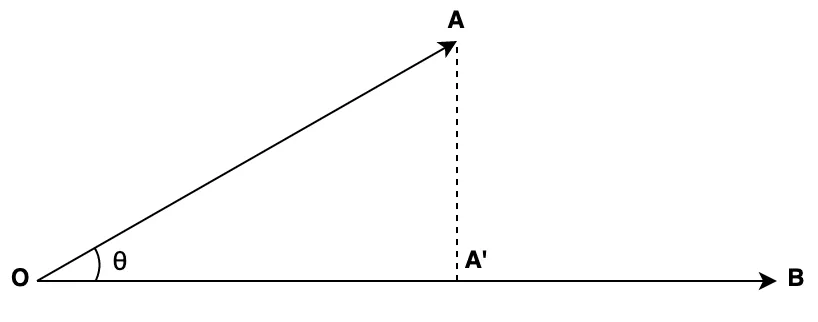
- OA: vector A
- OB: vector B
- OA’: the vector projection of A on B
\[ \cos(\theta) = \frac{OA’}{OA} \]
\[ \Rightarrow OA’ = \cos(\theta) \cdot OA \]
\[ \Rightarrow A \cdot B = OA’ \cdot OB \]
\[ \Rightarrow A \cdot B = \|A\| \|B\| \cos(\theta) \]
\[ \Rightarrow \cos(\theta) = \frac{A \cdot B}{\|A\| \cdot \|B\|} \]
3. Why do we need Cosine Similarity?
Cosine similarity is a powerful metric used to measure how similar two vectors are, regardless of their magnitude. It is widely used in Machine Learning, Natural Language Processing (NLP), recommendation systems, and many other fields.
3.1. A basic problem
Imagine a customer is searching for a smartphone in an online store. The system needs to find and rank the most relevant phone based on the query.
- Search query: “5G smartphone with great camera”
Your e-commerce store has the following two products:
- Product A: “5G smartphone with high resolution camera and long battery life”
- Product B: “Budget smartphone with dual camera and 4G connectivity”
The ouput: Your system should rank these two phones based on their relevance to the search query.
Let’s convert the query and products into vectors using a simple Bag of Words (BoW) representation. This approach creates a word frequency vector for each text.
3.1.1. Create a vocabulary
To convert text into vectors, we first create a vocabulary of unique words from all inputs:
| Index | Word |
|---|---|
| 1 | 5G |
| 2 | smartphone |
| 3 | with |
| 4 | great |
| 5 | camera |
| 6 | high-resolution |
| 7 | long |
| 8 | battery |
| 9 | life |
| 10 | budget |
| 11 | dual |
| 12 | 4G |
| 13 | connectivity |
3.1.2. Convert each text into a vector
- Query vector: \( Q = [1,1,1,1,1,0,0,0,0,0,0,0,0] \)
- Product A vector: \( A = [1,1,1,0,1,1,1,1,1,0,0,0,0] \)
- Product B vector: \( B = [0,1,1,0,1,0,0,0,0,1,1,1,1] \)
3.1.3. Calculate
Using cosine similarity formula, we have:
\[ \cos(Q, A) = 0.632 \]
\[ \cos(Q, B) = 0.507 \]
So, Product A (0.632) is more relevant to the search query than Product B (0.507) because it has a higher cosine similarity.
3.2. Applications of Cosine Similarity
3.2.1. Natural Language Processing (NLP)
- Used to compare text documents, search queries, and news articles.
- Helps find similar articles, or group related topics.
- E.g. A search engine compares your query vector with a database of document vectors using cosine similarity. The most similar documents are shown as top results.
3.2.2. Recommendation systems
- Measures how similar users or items are.
- Used in Netflix, YouTube, Spotify, and Amazon recommendations.
3.2.3. Image recognition
- Measures how similar two images are based on their feature vectors.
- Used for face recognition, object detection, and image search.
